E2: The (NP-Complete) Kids’ Game with the $2 Million Prize
The Eternity 2 (E2) puzzle has attracted the attention of puzzle fanatics, computer programmers, and mathematicians for many reasons, not the least of which is the $2 million prize for being the first to solve it. E2 is an edge-matching puzzle with 256 pieces. The general class of edge-matching puzzles is known to be NP-Complete, but it is unknown if there are aspects of E2 that can be exploited to make it tractable. In the spirit of cooperation, a few people have made their automated solvers available online, and I have provided an overview and back-of-the-napkin analysis of two of them.
Background
E2 has 256 square pieces that must be placed on a 16×16 grid. Each puzzle piece has 4 edges, each with one of 17 possible patterns, which must match the pattern of the neighbor piece that touches that edge. Each of the edges touching the border must be gray. There is also one hint piece which must be placed on the board at the indicated position and orientation.
The animation below shows a methodical approach to solving a 4×4 puzzle with no hint piece. Pieces are taken from the right side and placed on the board on the left. When a dead end is found and no more pieces can be placed on the board, pieces are removed up until the last decision point and a new piece is tried at that spot. The algorithm you are seeing in action is a backtracker.
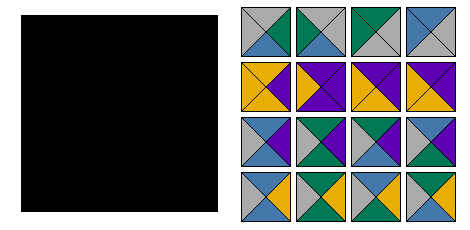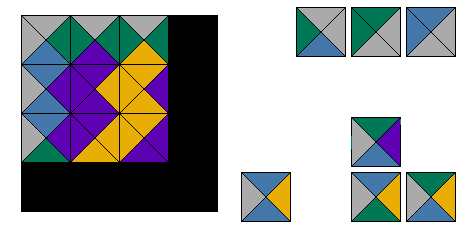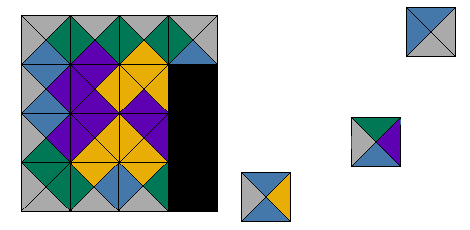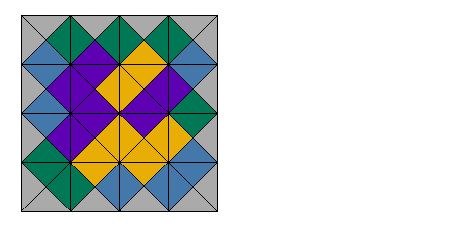
Clues & Rules
An additional hint is provided for solving each of the 4 clue puzzles, for a total of 5 possible hints. E2 clue puzzles I and III are 6×6, and E2 clue puzzles II and IV are 6×12. Clue puzzles III and IV are only available in the UK as of this writing. It is not required that the E2 solution use these optional hints, and it is suspected that E2 has more than one possible solution.
In order to win the $2 million prize, submit the solution to the Eternity 2 adjudicators by December 31. On the 31st, all entries will be opened and the entry that was submitted first wins the $2 million. Nobody submitted a complete solution in 2008 or 2009, so the competition will continue until December 31, 2010. A smaller prize may be awarded for the highest scoring partial solution if no complete solution was submitted. The complete rules can be found on the official site.
Sounds easy right? Well…
Solver Implementations
A few solvers have been made available online in the files section of the E2 Discussion Group. I picked two of the most straightforward solvers and ran benchmarks on them.
The first solver I looked at is Doc Smith’s C++ solver which is based on a solver by Marc Lebel. Doc’s solver works by first creating arrays that list the pieces that will have given colors on certain edges. This means that finding a piece with, say a green left edge and a red top edge, requires indexing the 2 dimensional array storing left and top matching pieces with the code for a green edge and the code for a red edge. The solver works by starting at the top left corner and tiling towards the bottom right corner (just like in the animation above), so there is no need for an array that would contain matches for say, only top and bottom edges. If the solver reaches a dead end, it backtracks recursively to the last decision point and tries again. Once the solver reaches the lower right corner, a solution has been found.
Next I looked Joel’s solver which is a Java port of the C++ backtrack solver written by Doc Smith. These two solvers work the same way; they differ only in the implementation language.
The E2 Discussion Group is very active and contains a lot of information on different solving strategies, so if you are interested in more advanced algorithms, have a look there.
 Benchmark Results
Benchmark Results
I ran benchmarks on both solvers to compare their performance. The benchmarks are puzzles similar in design to E2, but of a smaller size. I ran benchmarks on 6×6 with 1 hint, 8×8 with 2 hints, and 10×10 with 3 hints puzzles to get an idea of what kind of complexity we can expect from E2. All of the benchmarks were run on a dual core 2.00Ghz Intel with 1 GB of RAM. No compiler optimization flags were used for any of the test runs.
Here is a table giving the mean solution time for each of the solvers (the benchmarks had more than one possible solution, so I used the mean time in the table). On the 10×10 benchmark, I stopped the test after 10 hours. Neither of the solvers had found a solution at the time. The complexity of the puzzle increases exponentially in the number of pieces – this is to be expected of an NP-Complete problem.
| 6×6 | 8×8 | 10×10 | |
| Doc Smith | 891 msec | 91 min | 10+ hours |
| Joel | 790 msec | 107 min | 10+ hours |
One mildly surprising result is that the Java solver outperforms the C++ solver. Enough to make a difference solving the 16×16 E2 puzzle? Not likely. At this rate it would take more than a lifetime to find a solution for the 16×16. Improving the solving algorithm will give much better gains than code-level optimizations.
So will you get rich solving E2? Well, somebody will. If this type of challenge interests you, its definitely worth a shot.
 Resources:
Resources:
[Disclaimer: Links to amazon.com are affiliate links.]







Discussion on
E2: The (NP-Complete) Kids’ Game with the $2 Million Prize
by Jess Johnson in Fun Projects
55 Comments
2:56 pm UTC, 2009-06-24
5:16 am UTC, 2010-11-23
1:19 pm UTC, 2009-07-06
2:59 pm UTC, 2010-05-26
3:03 pm UTC, 2010-01-06
3:27 pm UTC, 2010-07-29
9:06 pm UTC, 2009-07-16
12:48 pm UTC, 2009-06-12
2:13 pm UTC, 2010-01-06
10:48 am UTC, 2010-05-26
6:06 am UTC, 2009-08-18
7:07 am UTC, 2010-01-05
7:14 am UTC, 2010-06-10
12:09 am UTC, 2010-03-11
7:26 pm UTC, 2008-06-29
9:03 pm UTC, 2009-12-30
10:05 am UTC, 2011-12-13
11:10 pm UTC, 2010-08-30
12:58 pm UTC, 2013-09-25
5:22 am UTC, 2009-08-25
3:27 am UTC, 2011-12-13
12:41 pm UTC, 2009-05-31
10:14 am UTC, 2009-05-31
8:15 pm UTC, 2008-12-19
1:38 pm UTC, 2009-05-31
9:41 am UTC, 2018-03-01
1:11 am UTC, 2009-07-30
2:46 pm UTC, 2009-06-12
12:07 pm UTC, 2010-01-03
10:49 am UTC, 2010-12-18
11:45 am UTC, 2010-01-03
10:05 am UTC, 2008-12-22
12:54 pm UTC, 2013-09-25
12:56 pm UTC, 2009-05-28
5:19 am UTC, 2010-01-05
1:55 pm UTC, 2009-05-31
7:06 am UTC, 2010-08-02
2:33 pm UTC, 2010-01-06
6:41 am UTC, 2010-08-30
12:13 am UTC, 2009-11-07
1:28 pm UTC, 2010-01-06
7:18 am UTC, 2008-12-18
3:05 pm UTC, 2008-06-02
12:46 am UTC, 2009-05-31
1:28 pm UTC, 2010-01-06_1_ 2W3 _4_
1:23 pm UTC, 2010-01-06X X X X XW3 3B1 1W4 4BX 4 3 2 1 4 3 2 1 XB1 1W3 3B1 1WX X X X X Style White Black 1 4 4 2 1 1 3 3 3 4 2 2Number of pieces must be even X:s aren't noted here because they dont got any pair. Thoughts: Maybe pieces could be sorted to two piles black and white. Then try to solve the piece locations. Number of possible pieces is only half of it used to be. 8x8x8x8x8 = 32768 But: 4x4x4x4x4 = 4096 This won't guarantine solution because there may be multiple even sorts of pieces..
6:25 am UTC, 2009-07-29
1:43 am UTC, 2009-11-13
6:41 am UTC, 2010-02-12
1:30 pm UTC, 2010-01-06
9:13 am UTC, 2009-01-20
4:48 pm UTC, 2009-01-27
11:39 pm UTC, 2009-05-31
10:23 am UTC, 2010-10-22
11:18 pm UTC, 2009-07-29Leave a reply